rightvisual.blogg.se - Compute z score

Each value in the body of the table is a cumulative area. The intersection of the rows and columns gives the probability or area under the normal curve.(The label for columns contains the second decimal of the z-score.)

The part of the z-score denoting hundredths is found across the top row of the table.

(The label in the row contains the integer part and the first decimal of the z-score.)

The left most column is how many standard deviations above (or below) the mean to one decimal place.

Which has a mean of 0 and a standard deviation of 1.

These tables are designed only for the standard normal distribution,.

A Z-Score Table, is a table that shows the percentage of values (or area percentage) to the left of a given z-score on a standard normal distribution. To find a specific area under a normal curve, find the z-score of the data value and use a Z-Score Table to find the area. Since the normal curve is symmetric about the mean, the area on either sides of the mean is 0.5 (or 50%).

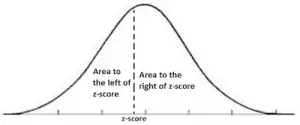
The total area under any normal curve is 1 (or 100%). The area percentage (proportion, probability) calculated using a z-score will be a decimal value between 0 and 1, and will appear in a Z-Score Table. Z-scores allow for the calculation of area percentages (also called proportions or probabilities) anywhere along a standard normal distribution curve (and, consequently along the corresponding normal distribution). What do we do when the value does not fall at an Empirical Rule subdivision? By using z-scores, we have the ability to locate a percentage (or area) under a standard normal distribution at any location. These subdivisions are fine for determining percentages as long as we are dealing with values that fall at these exact subdivision locations. We have seen that the Empirical Rule (68% - 95% - 99.7%) subdivides the area under a normal distribution into sections with widths of one standard deviation. The fact stated above is the reason we can find an area over an interval for any normal curve by finding the corresponding area under a standard normal curve (with a mean of 0 and a standard deviation of 1). (The term "area" will refer to "area percentage".) For example, the area percentage to the right of 1.5 standard deviations above the mean is identical for all normal curves. Areas under all normal curves are related.